تدریس خصوصی ریاضی
مقدمه
در جبرعموما لگاریتم معمولی یا لگاریتم در پایه ۱۰ عدد b را توانی تعریف میکنند که ۱۰ باید به آن برسد تا b بدست آید: 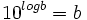 . فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم.
. فرض کنیم چنین عددی موجود بوده و از لگاریتمها برای سادهکردن ضرب اعدادی که ارقام اعشاری زیادی دارند استفاده میکنیم.
تعریف
تابع لگاریتم طبیعی 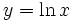 بصورت زیر نمایش داده میشود:
بصورت زیر نمایش داده میشود:
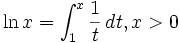
به ازای هر x بزرگتر از ۱ ، این انتگرال مساحت ناحیهای را نشان میدهد که از بالا به خم  از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است.
از پایین به محور t از طرف چپ به خط t=1 ، و از طرف راست به خط t=x محدود است.
تاریخچه
در اواخر قرن شانزدهم یک بارون اسکاتلندی به نام جان نپر (۱۵۵۰-۱۶۱۷) ابزاری بنام لگاریتم ابداع کرد که با تبدیل ضرب به جمع کار محاسبه را ساده میکند؛ یعنی داریم:
برای ضرب دو عدد مثبت x,a از یک جدول ، لگاریتمهای x,a را پیدا میکنیم، سپس این لگاریتمها را بهم میافزائیم مجموع حاصل را در داخل جدول مییابیم، و بالاخره حاصلضرب مطلوب ax را از حاشیه جدول میخوانیم. مسلما در دست داشتن جدول کلید کار بود، به همین سبب نپر در دو دهه آخر زندگیاش را صرف تهیه جدولی کرد که هیچگاه نتوانست آن را تمام کند. و این در حالی بود که تیکو براهه ستاره شناس ، مشتاقانه در انتظار این جدول بود تا میتواند محاسبات خودش را تسریع بخشد.
مشتق تابع لگاریتم طبیعی
چون تابع 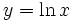 با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع
با انتگرال ذکر شده در قسمت تعریف ، تعریف میشود، فورا از نخستین قضیه اساسی حساب دیفرانسیل و انتگرال نتیجه میشود که مشتق تابع 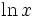 برابر
برابر 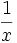 خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم:
خواهد بود. بنابراین اگر u تابع مشتقپذیری از x باشد، آنگاه از قاعده زنجیری داریم:
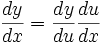
فرمول کلیتر زیر بدست میآید:
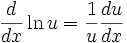
مشتقگیری لگاریتمی
گاهی یک تابع با معادلهای پیچیده داده شده با گرفتن لگاریتم از طرفین آن پیش از مشتقگیری میتوان مشتقش را سریعتر حساب کرد.
خواص 
- قلمرو: مجموعه تمام اعداد حقیقی مثبت ، x>0
- برد: مجموعه تمام اعداد حقیقی

- این تابع بر قلمرو خود پیوسته و صعودی است هر گاه
 آنگاه
آنگاه  . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است.
. این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است. - حاصلضرب ، خارج قسمت و توان: هر گاه x,a دو عدد مثبت باشند. آنگاه:
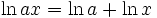
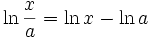
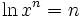
معکوس تابع لگاریتم
چون 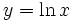 یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر
یکبهیک و مشتقپذیر است، دارای معکوس مشتقپذیر 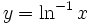 میباشد نمودار
میباشد نمودار 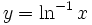 منعکس نمودار تابع
منعکس نمودار تابع 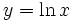 نسبت به خط y=x است. این نمودار تابع
نسبت به خط y=x است. این نمودار تابع 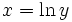 نیز میباشد. تابع
نیز میباشد. تابع 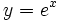 به ازای هر عدد حقیقی x مساوی
به ازای هر عدد حقیقی x مساوی 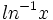 میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی
میباشد. تابع حاصل تابع مشتق پذیری از x است که به ازای هر x حقیقی 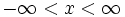 تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی که x بسمت منفی بینهایت میل میکند این حد برابر صفر میشود.
تعریف شده است و بعنوان تابع نمایی از آن یاد میشود که e را پایه و x نما خوانده میشود. همچنین توجه میکنیم که حد تابع نمایی زمانی که x بسمت بینهایت میل میکند برابر بینهایت است و زمانی که x بسمت منفی بینهایت میل میکند این حد برابر صفر میشود.
معادلات شامل 
چون این دو تابع معکوس یکدیگرند، به ازای هر 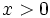 داریم:
داریم: 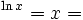
و به ازای هر x: 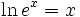
تابع  میزانهای نسبی رشد توابع
میزانهای نسبی رشد توابع
تعریف
وقتی a عدد مثبتی غیر از یک باشد. تابع 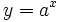 مشتقپذیر و یکبهیک است. لذا معکوس مشتقپذیر دارد که ما آن را لگاریتم x در پایه a نامیده و با
مشتقپذیر و یکبهیک است. لذا معکوس مشتقپذیر دارد که ما آن را لگاریتم x در پایه a نامیده و با 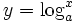 نشان میدهیم.
نشان میدهیم.
چون دو تابع ذکر شده در قسمت معکوس یکدیگرند بنابراین ترکیب آنها با هر ترتیبی تابع همانی میشود.
توجه میکنیم که لگاریتم x نمایی است که وقتی پایه به این نما میرسد x بدست میآید.
محاسبه 
عدد 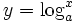 را همیشه میتوان از لگاریتمهای طبیعی x,a با فرمول زیر حساب کرد:
را همیشه میتوان از لگاریتمهای طبیعی x,a با فرمول زیر حساب کرد:
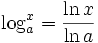
خواص 
خواص زیر مشابه خواص 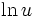 است و به آنی بدست میآید:
است و به آنی بدست میآید:
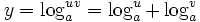
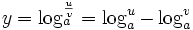
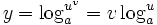
تبصره در باب نمادگذاری
در بسیاری از کتب پیشرفته و مقالات تحقیقی در ریاضی از 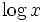 ، بدون ذکر پایه برای نمایش طبیعی
، بدون ذکر پایه برای نمایش طبیعی 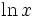 استفاده شده است. در بسیاری از کتب علوم طبیعی
استفاده شده است. در بسیاری از کتب علوم طبیعی 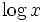 برای نمایش
برای نمایش 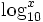 بکار رفته است. لگاریتم در پایه ۱۰ اغلب لگاریتم معمولی نامیده میشوند.
بکار رفته است. لگاریتم در پایه ۱۰ اغلب لگاریتم معمولی نامیده میشوند.
کاربردها
ابداع لگاریتم در قرن شانزدهم و هفدهم بزرگترین پیشرفت در حساب بوده است و قبل از اختراع کامپیوتر از مهمترین ابداعات بحساب میآید. لگاریتمها حسابدریانوردی را سامان بخشید. کاربرد آن را در علوم و مهندسی و همچنین نجوم نباید انکار کرد. بدین ترتیب که محاسبات اعشاری در نجوم ، دریانوردی و مثلثات را ممکن ساخت.
- لگاریتمهای معمولی اغلب در فرمولهای علمی بکار میروند مثلا: شدت زلزله بر حسب ریشتر توسط فرمول زیر بدست میآید:
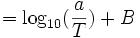
اندازه R
که در آن a دامنه حرکت زمین به میکرون در ایستگاه گیرنده و T دوره تناوب موج زلزله به ثانیه و B عاملی تجربی است که با افزایش فاصله از مرکز زلزله موجب تضعیف موج زلزله میشود.
- یکی دیگر از موارد استعمال لگاریتمهای معمولی عبارتند از واحد دسیبل برای سنجش شدت صوت.
- اندازهگیری واحد PH برای سنجش اسیدی بودن.

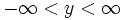
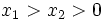 آنگاه
آنگاه 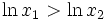 . این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است.
. این تابع یک تابع یکبهیک از قلمرو خود به بردش است، بنابراین دارای معکوس است.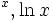
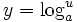 میزانهای نسبی رشد توابع
میزانهای نسبی رشد توابع