تدریس خصوصی ریاضی
مقدمه
هرگاه دامنه یک تابع را به چند جمله جدا از هم تقسیم کنیم، بطوری که اجتماع آن مجموعهها برابر با دامنه باشد ورودی هر مجموعه ، ضابطهای مجزا تعریف کنیم، در این صورت یک تابع چندضابطهای بدست میآوریم. تابع قدرمطلق یکی از انواع توابع چند ضابطهای است.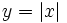
ویژگیهای تابع قدرمطلق
- قدرمطلق عددی مانند
 ، عدد
، عدد  است. اگر
است. اگر  مثبت باشد قدرمطلق آن همان
مثبت باشد قدرمطلق آن همان  است. ولی اگر منفی باشد قدرمطلق
است. ولی اگر منفی باشد قدرمطلق  و اگر صفر باشد قدرمطلقش صفر خواهد شد.
و اگر صفر باشد قدرمطلقش صفر خواهد شد. - قدرمطلق حاصلضرب دو عدد ، حاصلضرب قدرمطلقهای آن است با استفاده از علائم میتوان نوشت:
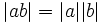
- قدرمطلق مجموع دو عدد هیچگاه بزرگتر از مجموع قدرمطلقهای آن نیست. اگر این نابرابری را توسط علائم بیان کنیم یک نابرابری بدست میآوریم که به نابرابری مثلثی معروف است:
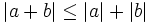
- قدرمطلقها ، فواصل بین نقاط روی محورها را بدست میدهند.
- از قدرمطلقها برای تعریف بازهها نیز استفاده میشود. بعبارت دیگر رابطه بین قدرمطلق و فاصله به ما این امکان را میدهد که نابرابریهای قدرمطلقی را برای مشخصکردن بازهها بکار بریم. برای مثال معنی عبارت زیر برابر است با:
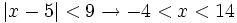
رسم تابع قدرمطلق
همانطور که گفتیم منظور از قدرمطلق  ، اندازه
، اندازه  است. نمودار این تابع را با استفاده از تعریف قدرمطلق بدست میآوریم. همانطور که از تعریف بدست میآید این نمودار برای
است. نمودار این تابع را با استفاده از تعریف قدرمطلق بدست میآوریم. همانطور که از تعریف بدست میآید این نمودار برای 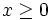 برابر
برابر  است یعنی برای
است یعنی برای  های مثبت نمودار
های مثبت نمودار 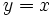 را رسم میکنیم. همینطور در تعریف داریم برای
را رسم میکنیم. همینطور در تعریف داریم برای 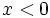 ،
، 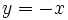 . بنابراین برای
. بنابراین برای  های منفی نمودار
های منفی نمودار 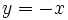 را رسم خواهیم کرد. یا بعبارت بهتر برای
را رسم خواهیم کرد. یا بعبارت بهتر برای  های مثبت نیمساز ربع اول و برای
های مثبت نیمساز ربع اول و برای  های منفی نیمساز ربع دوم مدنظر ترسیم ماست. که شکل آن بصورت روبهرو بدست میآید.
های منفی نیمساز ربع دوم مدنظر ترسیم ماست. که شکل آن بصورت روبهرو بدست میآید.
اگر این نکته را مورد توجه قرار دهیم که تابع 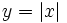 زوج است (زیرا
زوج است (زیرا 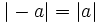 آنگاه نیمه دوم نمودار این تابع (برای مقادیر منفی
آنگاه نیمه دوم نمودار این تابع (برای مقادیر منفی  ) را میتوان از نیمه اول آن بدست آورد. (برای یادآوری تابع زوج مراجعه کنید به مقاله انواع تابع ). نکتهای که ذکر شد به معنای آن است که نمودار این تابع نسبت به محور
) را میتوان از نیمه اول آن بدست آورد. (برای یادآوری تابع زوج مراجعه کنید به مقاله انواع تابع ). نکتهای که ذکر شد به معنای آن است که نمودار این تابع نسبت به محور 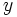 ها تقارن دارد و نیمه دوم آن را میتوان از تقارن نیمه اول نمودار نسبت به محور
ها تقارن دارد و نیمه دوم آن را میتوان از تقارن نیمه اول نمودار نسبت به محور 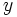 ها بدست آورد.
ها بدست آورد.
گاه اتفاق میافتد که به هنگام ترسیم با توابعی سروکار داریم که داخل قدرمطلق تنها  قدر ندارد مثل
قدر ندارد مثل  نمودار اینگونه توابع را میتوان از روی تابع
نمودار اینگونه توابع را میتوان از روی تابع 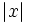 بدست آورد. اگر
بدست آورد. اگر 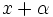 بود در اینصورت نمودار به اندازه
بود در اینصورت نمودار به اندازه 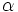 بسمت چپ انتقال مییابد روی محور
بسمت چپ انتقال مییابد روی محور  ها. اگر
ها. اگر 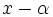 بود آنگاه نمودار
بود آنگاه نمودار 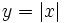 به اندازه
به اندازه 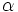 بسمت ر است انتقال مییابد.
بسمت ر است انتقال مییابد.
گاهی اوقات نیز بصورت 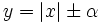 ظاهر میشود. که در آنصورت به طریقی که ذکر میشود برخورد میکنیم. نمودار
ظاهر میشود. که در آنصورت به طریقی که ذکر میشود برخورد میکنیم. نمودار 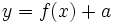 به انتقال
به انتقال 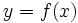 به اندازه
به اندازه 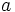 واحد در امتداد محور
واحد در امتداد محور 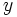 ها بدست میآید. جهت انتقال توسط علامت
ها بدست میآید. جهت انتقال توسط علامت 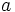 مشخص میشود. بطوری که اگر
مشخص میشود. بطوری که اگر 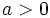 بود آنگاه نمودار به سمت بالا منتقل میشود و اگر
بود آنگاه نمودار به سمت بالا منتقل میشود و اگر 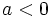 نمودار بسمت پایین منتقل میگردد. این نکته در رسم نمودار تمامی توابع کاربرد دارد که تابع قدرمطلق یکی از آنهاست.
نمودار بسمت پایین منتقل میگردد. این نکته در رسم نمودار تمامی توابع کاربرد دارد که تابع قدرمطلق یکی از آنهاست.
- برای رسم توابعی بصورت
 با دو تبدیل رسم را انجام میدهیم:
با دو تبدیل رسم را انجام میدهیم:
- انتقال در امتداد محور
 ها
ها - یک کشش در امتداد محور
 ها.
ها.
برای مشخصکردن مقدار انتقال لازم است تا ابتدا ضریب  را به جلوی علامت قدرمطلق منتقل کنیم:
را به جلوی علامت قدرمطلق منتقل کنیم:
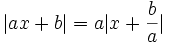
برای بدستآوردن نمودار تابع 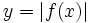 با استفاده از نمودار تابع
با استفاده از نمودار تابع 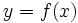
لازم است بخشهایی از نمودار
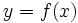
را که بالای محور
 .هاست بدون تغییر نگه داریم و بخشهایی که پایین محور
.هاست بدون تغییر نگه داریم و بخشهایی که پایین محور  هاست نسبت به محور
هاست نسبت به محور  انعکاس دهیم
انعکاس دهیم

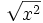 است. اگر
است. اگر 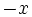 و اگر صفر باشد قدرمطلقش صفر خواهد شد.
و اگر صفر باشد قدرمطلقش صفر خواهد شد.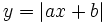 با دو تبدیل رسم را انجام میدهیم:
با دو تبدیل رسم را انجام میدهیم: